Artigo Científico

 

Os modelos mentais de frações: como universitários lidam com conceitos fundamentais de matemática?

 

Mental models of fractions: how undergraduates deal with fundamental concepts of mathematics?

 

 

Niltom Vieira Junior^I; Laurence Duarte Colvara^II

^IInstituto Federal de Educação, Ciência e Tecnologia de Minas Gerais (IFMG), Formiga, Minas Gerais, Brasil;
^IIUniversidade Estadual Paulista (UNESP), Ilha Solteira, São Paulo, Brasil

 

 

---

Resumo

Este trabalho apresenta uma investigação realizada com alunos dos cursos superiores do Instituto Federal de Educação, Ciência e Tecnologia de Minas Gerais (IFMG) - Campus Formiga. Ao identificar os modelos mentais de estudantes de ciências exatas perante um tema fundamental de matemática, neste caso as frações, observaram-se fatos importantes: os alunos podem utilizar diferentes estratégias, equivalentes conceitualmente, para resolver um mesmo problema; nem sempre as melhoras notas, segundo métodos tradicionais de avaliação, condizem com aqueles cujo domínio conceitual é mais aprimorado; e as metodologias de ensino utilizadas pelos professores podem influenciar toda a vida acadêmica dos alunos, alimentando seu sistema de crenças. Deste modo, realiza-se uma discussão quanto às estratégias utilizadas no ensino de matemática, principalmente no que diz respeito ao desenvolvimento conceitual e aos métodos de avaliação, o que reforça a responsabilidade da atuação docente na sala de aula. © Cien. Cogn. 2010; Vol. 15 (1): 124-136.

Palavras-chave: modelos mentais; educação em ciências e matemática; métodos de avaliação.

---

Abstract

This work presents an investigation with undergraduate students from Federal Institute of Minas Gerais (IFMG) - Campus Formiga. After identifying the mental models of a fundamental subject in math, fractions, important facts were observed: students may use different strategies to solve the same problem; not always the best grades, according to traditional methods of evaluation, are consistent with those students whose conceptual domain is larger; and the teaching methods may prejudice the whole academic life of students, influencing their system of beliefs. So, is presented a discussion about teaching strategies, particularly in relation to conceptual development and evaluation methods, which increases the responsibility in the classroom. © Cien. Cogn. 2010; Vol. 15 (1): 124-136.

Keywords: mental models; science and math education; methods of evaluation.

---

 

 

Introdução

As concepções tradicionais de ensino refletem um modelo organizativo e disciplinador, no qual a transmissão do conhecimento segue padrões pré-elaborados, sendo os principais recursos as aulas expositivas e a utilização de livros-texto. O professor explica os conteúdos, os alunos fazem suas anotações com rara participação em aula e estudam para prova, que em alguns casos avalia apenas a capacidade de memorizar e repetir os conceitos vistos em exercícios de fixação (Vieira Junior e Colvara, 2006). O problema desta sequência de ações é que, por vezes, o aprendizado pode não ocorrer, sendo o aluno avaliado por sua habilidade em se adequar a um processo simples e mecânico de transpor informações.

Portanto, aprender a refletir, a raciocinar, a utilizar estratégias mais bem elaboradas para resolver problemas e a melhor utilizar os recursos cognitivos de forma a contribuir com a formação acadêmica, tem se tornado um dos grandes desafios da escola.

Muitos questionamentos relacionados à cognição e a sua influência nas relações de ensino-aprendizagem vem ocorrendo ao longo do tempo, o que tem despertado uma perspectiva inovadora de ensino baseada em características não antes utilizadas. Todavia a "educação cognitiva" propriamente, embora possua uma extensa herança histórica, não tem sido ainda efetivamente utilizada nas salas de aula e nos currículos de ensino (Fonseca, 2009).

Considerando que esta nova corrente pedagógica tende a estreitar as relações entre a teoria e prática, a formar professores críticos em relação aos seus métodos de ensino e a realizar intervenções com maior base científica, este trabalho promove contribuições iniciais a este novo paradigma na medida em que apresenta os resultados de uma investigação realizada com os alunos, escolhidos aleatoriamente, dos cursos de licenciatura em matemática, tecnologia em gestão financeira e engenharia elétrica do Instituto Federal de Minas Gerais - Campus Formiga.

Com fins de promover evidências empíricas da influência dos educadores no processo de ensino-aprendizagem, assim como das habilidades cognitivas no desenvolvimento escolar, levanta-se a hipótese de que estudantes em todos os níveis de ensino, inclusive universitários, utilizam diferentes estratégias de raciocínio para resolver um mesmo problema, mesmo ao se trabalhar com conceitos matemáticos considerados fundamentais.

Para isto assumiu-se o pressuposto, indicado por Gardner (2003), de que a atividade cognitiva humana deve ser descrita em termos de símbolos, esquemas, imagens ou outras formas de representação mental. Moreira (1997), por exemplo, sugere que o funcionamento da mente seja mais bem entendido em termos de representações e procedimentos computacionais que atuem sobre tais representações.

Existem, porém, divergências no que diz respeito ao processamento das informações. Alguns acreditam na existência de uma única forma de representação que é do tipo digital (baseada em proposições e/ou uma espécie de código mental), outros acreditam em pelo menos duas, a digital e a analógica (baseada em imagens determinadas pelos sentidos), e há ainda aqueles que crêem na existência de múltiplas possibilidades representacionais.

Considerando que discordâncias a este respeito serão sempre encontradas, em razão principalmente da grande interdisciplinaridade envolvida nas ciências cognitivas, este estudo parte de uma perspectiva mais objetiva que se abstém a polêmica imagem/proposição traçada na psicologia cognitiva e propicia possíveis diagnósticos/intervenções mais acessíveis. Trata-se da teoria dos Modelos Mentais, um terceiro construto que, embora tenha se originado há várias décadas, disseminou-se principalmente a partir da publicação de dois livros intitulados "Mental Models" em 1983. O primeiro deles editado por Gentner e Stevens (1983) é uma coleção de trabalhos publicados em um seminário sobre o assunto. O segundo, de Johnson-Laird (1983), é um trabalho em que o autor busca explicar o raciocínio dedutivo e a compreensão de textos via modelos mentais.

Os modelos mentais sintetizam ambas as possibilidades representacionais ao postular que um modelo mental pode ser totalmente analógico ou, parcialmente analógico e parcialmente proposicional.

Ainda que em um nível básico o cérebro possa computar os modelos e as imagens em algum código específico, o uso destas representações libera a cognição da obrigação de operar proposicionalmente (Moreira, 1997). Portanto de modo análogo às linguagens de programação de alto nível, que em tempo de compilação são traduzidas pelo computador em código binário, os modelos mentais se tornam representações facilitadoras, e não menos científicas, para o entendimento da cognição humana.

Eysenck e Keane (2007) classificam a abordagem dos modelos mentais como uma das teorias mais influentes a respeito do raciocínio dedutivo, onde as pessoas os constroem a partir de premissas e os utilizam para extrair conclusões. De modo mais simples, Johnson-Laird (1983) afirma que um modelo mental representa um possível estado de coisas do mundo. Embora estes modelos não se restrinjam as distribuições espaciais, um exemplo concreto é apresentado em Eysenck e Keane (2007):

"Premissas
A lâmpada está à direita da almofada.
O livro está à esquerda da almofada.
O relógio está na frente do livro.
O vaso está na frente da lâmpada.
Conclusão
O relógio está à esquerda do vaso."

Segundo Johnson-Laird (1983), baseado nas premissas acima, pode-se construir um modelo mental simples e não ambíguo como o apresentado na figura 1.

 

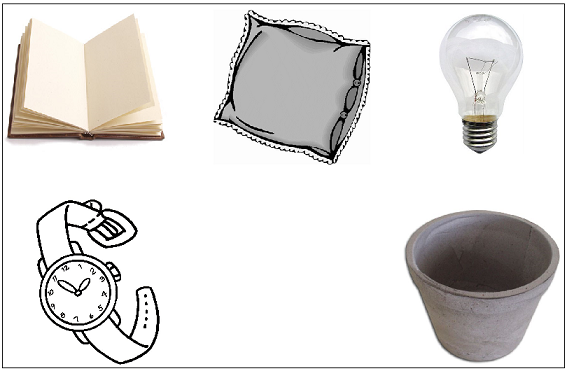
Figura 1 - Organização espacial.

 

Para ele, ao invés de uma lógica mental, o ser humano apropria-se da combinação de modelos mentais para raciocinar, que na forma de blocos de construção cognitiva podem ser combinados e recombinados. Neste sentido, o desenvolvimento do raciocínio dedutivo está não somente na construção dos modelos, mas na lógica utilizada para verificar e testar as conclusões a partir destas combinações.

Entretanto, em alguns casos a combinação (ou imprecisão) de enunciados pode admitir mais de um estado. Fica claro que argumentos que envolvem apenas um modelo mental podem ser resolvidos com exatidão, por outro lado a ocorrência de múltiplos modelos, sejam eles produtos das premissas ou sejam eles necessários por se trabalhar com sistemas complexos, torna mais difícil a realização de testes, o estabelecimento de conclusões e a resolução dos problemas. Este fato coincide com a suposição incorporada à teoria, e posteriormente evidenciada por Johnson-Laird (1999), de que a capacidade das pessoas de construir modelos mentais é restringida pela capacidade limitada da memória de trabalho.

Existem posições contrárias ao pressuposto de Johnson-Laird (1983) de que modelos mentais são análogos estruturais do mundo, como por exemplo, a apresentada em um estudo realizado por Ford (1995) onde as pessoas deviam dizer em voz alta o que pensavam enquanto resolviam silogismos. Dentre o grupo de estudo, notou-se que 40% dos participantes utilizavam o raciocínio espacial e 35% utilizavam o raciocínio verbal. Para Ford (1995) nestes casos não se constatou evidências de que um análogo estrutural havia sido construído. Entretanto, levanta-se aqui a hipótese de que características como as apresentadas em teorias sobre perfis psicológicos podem exercer influência no que tange a estas diferenças individuais.

De todo modo faz-se algumas ressalvas. Primeiro que, segundo Eysenck e Keane (2007), a teoria dos modelos mentais considera o desempenho do raciocínio em uma variada extensão de problemas e a maioria de suas hipóteses tem sido confirmada empiricamente. Destaca-se, também, o forte argumento de que muitos dos erros verificados nas tarefas de raciocínio dedutivo possam ser atribuídos ao fato que Johnson-Laird (1999) chamou de princípio da verdade: "os indivíduos minimizam a carga na memória de trabalho tendendo a construir modelos mentais que representem explicitamente apenas o que é verdadeiro".

Além disto, outros autores apresentam concepções relativamente distintas daquelas propostas por Johnson-Laird (1983). Borges (1997) define o que seria um "modelo mental" das diversas concepções sobre modelos mentais, utilizando camadas. As mais externas possuem pressupostos mais restritos como, por exemplo, a definição de que são estruturalmente análogos aos sistemas que eles representam. Em um nível anterior supõe-se que as pessoas façam inferências manipulando seus modelos mentais e simulando-os simbolicamente como se fossem um programa de computador. Brewer (1987) destaca, também, que as estruturas de Johnson-Laird (1983) são construídas e utilizadas no momento em que se lida com as tarefas, enquanto àquelas definidas por Gentner e Stevens (1983), por exemplo, seriam mais genéricas e relacionadas à causalidade em sistemas (embora não haja nada que restrinja a existência prolongada de um modelo na concepção de Johnson-Laird). Gentner e Gentner (1983), por sua vez, empregam o conceito de modelo mental mais ligado às analogias, e assim por diante.

De todo modo, a idéia de "processar" um modelo mentalmente e a partir de então realizar tarefas parece comum nas diversas abordagens. Foi a configuração destes sistemas "executáveis" que se buscou identificar neste trabalho, associando suas características aos eventuais sucessos ou fracassos na resolução dos problemas envolvendo frações. Sugere-se ainda, em comum acordo com Borges (1998), que parte das inconsistências verificadas nestes modelos sejam resultado de intervenções mal elaboradas por um ou mais professores que o estudante possa ter ao longo da vida escolar.

Neste ponto nota-se a distinção definida por Norman (1983) entre modelos mentais (representações internas) e modelos conceituais (instrumentos apresentados para compreensão de sistemas). O modelo conceitual deve configurar-se como uma "interface" precisa, consistente e completa em relação ao sistema a ser estudado, projetada pelo professor para facilitar o entendimento e proporcionar a construção de modelos mentais. Dentre os fatores funcionais que se aplicam na elaboração de modelos (conceituais ou mentais) destaca-se o sistema de crenças. Segundo Norman (1983), modelos mentais individuais refletem crenças sobre um sistema, que podem ser adquiridas por observação, inferência ou instrução. Portanto estratégias inadequadas, ou insuficientes, além de não promoverem o conhecimento podem, em situações extremas, constituir crenças que comprometam o desempenho do estudante na sua progressão acadêmica.

Para melhor identificar estes aspectos e levantar evidências que corroborassem com tais hipóteses, definiu-se então uma metodologia para a investigação.

 

Metodologia

Considerando todos os aspectos já mencionados, após a realização de um extenso estudo sobre cognição (Sternberg, 2008; Eysenck e Keane, 2007; Fonseca, 2009), sobre a teoria dos modelos mentais a luz de alguns autores (Borges, 1997; Moreira, 1997; Johnson-Laird, 1983; Gentner e Stevens, 1983) e de protocolos de investigação utilizados em outras experiências (Borges, 1998; Barbosa e Borges, 2006; Lagreca e Moreira, 1999; Moreira e Oliveira, 2003), definiram-se as estratégias metodológicas pelas quais se daria a investigação sobre o tema "Frações". Foram analisados vinte e dois (22) alunos dos seguintes cursos superiores oferecidos pelo IFMG (Instituto Federal de Minas Gerais): licenciatura em matemática (12), tecnologia em gestão financeira (07) e engenharia elétrica (03). Tal pesquisa foi realizada com anuência da Secretaria de Ensino desta instituição e dos alunos envolvidos, sendo os mesmos informados a respeito da finalidade do estudo.

Foi elaborado um questionário composto por onze (11) questões, sendo nove (9) questões abertas e duas (2) de verdadeiro ou falso. Depois de respondido, o questionário era lido na presença do entrevistado e as respostas dadas direcionavam uma entrevista na qual se desejava identificar a estratégia e raciocínio utilizados para solução dos problemas. Este diálogo foi gravado, para que os dados pudessem ser posteriormente analisados com maior clareza baseado na teoria de Johnson-Laird (1983). Quando necessário, faziam-se também anotações sobre dúvidas e comentários feitos pelos entrevistados. Ao término desta etapa, os estudantes foram orientados a construir um mapa conceitual abrangendo tudo o que achassem relevante sobre seu conhecimento acerca do assunto. Trata-se de uma técnica para visualizar a organização do conhecimento, fundada na teoria do aprendizado significativo. Em síntese é uma representação gráfica como, por exemplo, um organograma construído de modo que as relações entre diferentes conceitos sejam evidentes. Abaixo, pode ser visto o mapa conceitual desenvolvido por um dos alunos durante a realização da entrevista (figura 2).

 

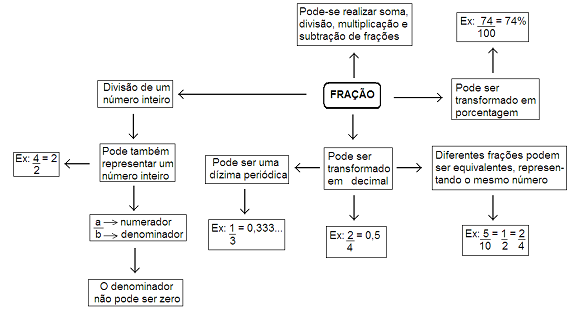
Figura 2 - Mapa conceitual construído por um dos alunos.

 

A definição dos modelos identificados, assim como as conclusões deste trabalho, foram feitas com base no confronto de todos estes dados. A seguir apresenta-se o questionário utilizado no estudo.

1) Ao se falar em Fração, o que vem a sua cabeça?

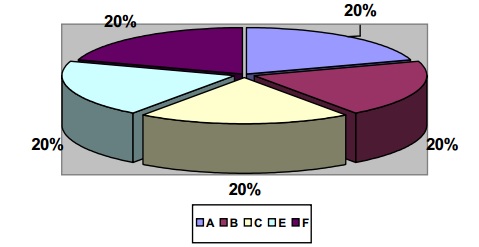
2) Observe o gráfico abaixo:

 

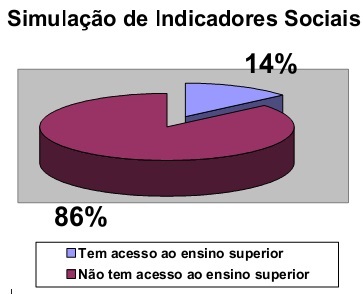
Figura 3 - Indicadores sociais.

 

Com base nos dados fornecidos pelo gráfico, é possível mostrar estes mesmos dados em algum outro formato que não seja em porcentagem? Se possível mostre qual formato.

3) Existe alguma relação entre os números mostrados abaixo? Se existir fale sobre esta relação:

7/20 0,35 35%

4) Escreva um número decimal qualquer. Escreva, também, este número por extenso.

5) Cada área colorida em cada círculo representa uma fração de um inteiro. Qual a soma destas frações?

 

Figura 4 - Soma de frações.

 

6) Qual outra representação da dízima periódica 0,555...?

7) Fale sobre a relação entre os itens mostrados logo abaixo.

a) O gráfico:

 

Figura 5 - Relação entre frações e porcentagens.

 

b) 1/5

c) 0,05

8) Qual outra representação da dízima periódica 1,15444...?

9) Ao lançar um dado, qual a probabilidade de a face voltada para cima corresponder ao número 3?

As questões a seguir foram extraídas do livro "Para aprender matemática" (Lorenzato, 2008).

10) Das afirmações seguintes, assinale com V aquelas que você julgar verdadeiras e com F as falsas:

( ) 1. Em nosso cotidiano não utilizamos frequentemente os números fracionários.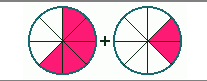
( )2. Frações diferentes sempre representam quantidades diferentes.
( )3. Sempre que um número estiver na forma fracionária, significa que não se trata de um número inteiro.
( )4. Qualquer número fracionário é sempre menor que 1 (inteiro).
( )5. O único modo correto para adicionar duas frações com denominadores diferentes é calcular o mínimo múltiplo comum (mmc) dos denominadores.
( )6. O único procedimento correto para dividir duas frações é multiplicar a primeira delas pelo inverso da segunda.
( )7. O produto de duas frações, diferentes de zero, é sempre menor que elas.
( )8. O quociente de duas frações, diferentes de zero, é sempre menor que elas.

Dos conceitos seguintes, assinale com X aqueles que se relacionam com o conceito de fração:

 

( ) probabilidade ( ) par ordenado ( ) razão ( ) comparação ( ) taxa

( ) divisão ( ) número decimal ( ) velocidade ( ) medida ( ) operador

( ) inclinação ( ) porcentagem ( ) proporção ( ) número racional ( ) classe de equivalência

 

Resultados

Após análise do material coletado observou-se a existência de dois grupos: um considerado como não-modelador (que não possuía nenhum modelo mental); e outro no qual foi identificada a existência de quatro (4) diferentes modelos, que atendiam a distintos níveis conceituais.

Os que pertenciam ao primeiro grupo enxergavam frações como um "numerador sobre um denominador" apenas. Ou um número sobre outro, referenciando-se sempre a definição mais simples que se pode dar a este conteúdo. Este modelo foi verificado em 9% dos entrevistados, que em muitos casos conseguiam responder as questões, porém, de forma mecânica. Quando inquiridos sobre o porquê de se resolver daquele modo, respondiam apenas que fora assim que haviam aprendido, o que levou a conclusão que alguns haviam memorizado um algoritmo de resolução sem nenhum preceito conceitual.

Quanto aos pertencentes ao segundo grupo, observou-se que a maioria dos alunos ao ser interrogada a respeito de sua primeira impressão sobre frações relacionava o tema a divisibilidade. Também se pode perceber uma grande dificuldade dos entrevistados com relação às questões sobre dízimas periódicas. Todavia, de posse dos dados analisados foram encontrados os seguintes modelos mentais:

• Fração como divisão: os que compunham este grupo associavam fração principalmente, ou em primeiro lugar, à divisão. Sendo esta a principal relação estabelecida por 59% dos entrevistados para resolver os problemas;
• Fração como parte: 23% dos entrevistados associavam fração como "parte de algo". Diferentemente do primeiro modelo, estas pessoas não encaravam fração como divisão, mas sim como parte ou pedaço de alguma coisa;
• Fração como razão e proporção: presente em 4,5% dos entrevistados este modelo apresentou-se mais elaborado que os anteriores. Um indivíduo neste grupo além de relacionar fração como a razão entre dois números, mantinha a noção de proporcionalidade entre os mesmos;
• Modelo científico: este modelo encontrado em 4,5% dos indivíduos corresponde ao nível máximo que se pretendia observar para o escopo avaliado. O membro desta categoria possuía uma visão integradora estabelecendo relações entre todos os conceitos presentes nos modelos anteriores.

O entrevistado pertencente a este último modelo, tido como científico, apresentou também maior agilidade ao prover respostas e justificativas. Ao ser questionado, por exemplo, sobre as relações existentes em um gráfico que só exibia valores percentuais, um número em forma de fração e um número decimal (Questão 7), respondeu instantaneamente quais situações poderiam ser descritas por frações, enumerou as relações possíveis e demonstrou como isto poderia ser feito. A distribuição detalhada de ocorrências por categorias pode ser vista na figura 6.

 

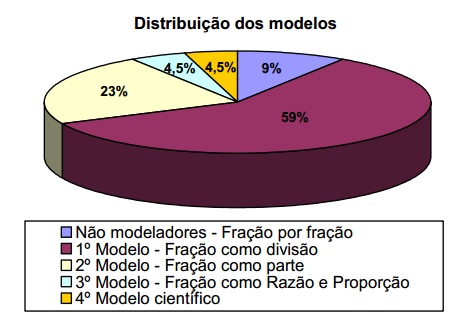
Figura 6 - Distribuição dos modelos.

 

Discussão

Ao se considerar apenas a quantidade de acertos, o que normalmente se avalia no sistema tradicional de avaliação, observaram-se ainda outros fatos interessantes. O indivíduo classificado no modelo científico, como era de se esperar, foi o único a acertar todos os itens justificando-os coerentemente. Entretanto, a distribuição observada para os demais entrevistados chamou a atenção.

Na elaboração do questionário, buscou-se a utilização de questões com graus equilibrados de dificuldade, com o intuito de se verificar exclusivamente as estratégias e modelos adotados para resolução dos problemas - considerando ainda o fato de se tratar de uma abordagem, em tese, elementar para estudantes universitários. Todavia, confirmaram-se evidências das duas hipóteses previamente levantadas:

1º - As diferenças individuais contribuem em algum aspecto para a formulação de distintas estratégias (ou modelos) utilizadas na resolução de problemas. Isto significa que, ao menos em determinada faixa de desempenho, os alunos podem atingir os mesmos resultados por diferentes meios. Esta afirmação reforça a idéia de que considerar perfis psicológicos nas intervenções educacionais pode promover o equilíbrio, na medida em que auxilia a construção do conhecimento de alunos com maiores dificuldades;

2º- Os métodos tradicionais de avaliação nem sempre condizem com o real conhecimento dos alunos.

Para ilustrar estes fatos foram atribuídos os conceitos A, B, C, e D conforme a quantidade de itens respondidos corretamente no questionário (incluindo a realização coerente do mapa conceitual):

• Conceito A: 12 acertos;
• Conceito B: 09 a 11 acertos;
• Conceito C: 06 a 08 acertos;
• Conceito D: 03 a 05 acertos.

 

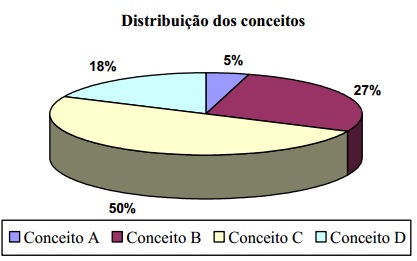
Figura 7 - Distribuição dos conceitos.

 

No gráfico abaixo (figura 8) pode-se observar claramente que indivíduos com diferentes estratégias de raciocínio obtiveram a mesma "nota" (1º e 2º modelos, para o conceito C; e 1º, 2º e 3º para o conceito B), conforme a pontuação distribuída, comprovando a hipótese primeira.

 

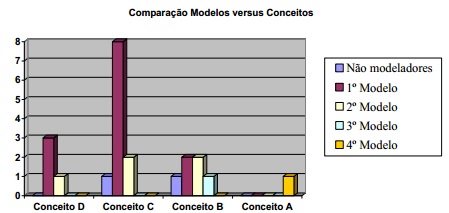
Figura 8 - Modelos versus conceitos.

 

Constatam-se também casos em que indivíduos não-modeladores, assim classificados pela ausência de base conceitual e uso de técnicas mecanicistas para resolução de problemas, obtiveram melhor avaliação (conceito B) que elementos classificados nos modelos 1 e 2, cujo conhecimento foi comprovadamente melhor identificado. Este fato comprova a hipótese segunda.

Merece atenção ainda o fato que dentre os licenciandos em matemática 8% dos entrevistados foram classificados como não-modeladores, a maioria de 67% correspondeu ao primeiro modelo, 17% ao segundo modelo, 8% ao terceiro modelo e nenhum entrevistado deste curso configurou-se no modelo científico. Embora a amostragem utilizada não seja suficiente para afirmações generalizadas neste quesito, os índices são interpretados como preocupantes considerando que os alunos da licenciatura, em especial, serão responsáveis pela formação daqueles que em um futuro próximo estarão também na universidade. Destaca-se que todos os cursos desta instituição encontram-se na primeira turma, mas, no caso da licenciatura em matemática, excluindo-se os quatro alunos que contribuíram com as entrevistas, todos foram entrevistados.

 

Considerações finais

Ao investigar os modelos mentais para um tema considerado fundamental, ao menos para alunos universitários provenientes das ciências exatas, diversas conclusões puderam ser observadas.

Primeiramente notou-se que a maioria dos alunos encontra-se distante do nível conceitual esperado para eles, visto através dos seus modelos mentais, e que em raros casos eles possuem múltiplas visões para um mesmo problema. Em contrapartida, constatou-se também que diferentes modelos podem ser utilizados para se chegar aos mesmos resultados. Este aspecto denota a influência que características individuais exercem no raciocínio. Ressalta-se que estas características podem ser usadas a favor do ensino, desde que os professores as reconheçam e as utilizem para promover a evolução dos modelos mentais daqueles alunos, cuja metodologia inicialmente adotada não tenha contribuído suficientemente.

Por outro lado, destacam-se também as evidências de que os métodos de avaliação tradicionalmente utilizados nem sempre mensuram o nível de conhecimento conceitual dos alunos. Exemplo disto foi o fato de um não-modelador obter o conceito B (baseado apenas no número de questões respondidas corretamente), enquanto diversos alunos identificados nos modelos 1 e 2 obtiveram avaliação inferior.

Por fim, se para um assunto tão trivial foram observadas falhas conceituais, parte delas possivelmente originadas das estratégias de ensino e sistemas de crenças transmitidos pelos professores aos alunos nos primeiros anos de escolaridade, o fato se agrava ao imaginar que o mesmo pode se repetir com conhecimentos mais complexos, como aqueles em que estes mesmos alunos estejam lidando atualmente nos seus respectivos cursos de graduação.

Embora a conclusão se aplique ao grupo estudado, acredita-se que alguns destes fatos possam ser generalizados. Por esta razão torna-se de extrema importância a reflexão e adequada intervenção docente baseado na influência que sua atuação pode exercer na futura carreira de seus alunos, sejam eles licenciados, bacharéis ou tecnólogos. Assume-se, portanto, que conhecer as individualidades e modelos mentais dos alunos ao lidar com um tema específico, possibilita procedimentos de ensino melhor elaborados. Foi isto que esta investigação buscou realizar para o tema "Frações".

 

Agradecimentos

Os autores agradecem aos alunos Alfredo Valadão, Clayton Pereira, Daniela Alves e Mayra Camargo, do curso de licenciatura em matemática, pelo apoio na realização das entrevistas e contribuição ao ensino de ciências e matemática.

 

Referências Bibliográficas

Barbosa, J.P.V. e Borges, A. T. (2006). O entendimento dos estudantes sobre energia no início do ensino médio. Caderno Brasileiro de Ensino de Física, 23, 182-217.         [ Links ]

Borges, A.T. (1997). Um estudo de modelos mentais. Investigações em ensino de ciências, 2(3), 207-226.         [ Links ]

Borges, A.T. (1998). Modelos mentais de eletromagnetismo. Caderno Catarinense de Ensino de Física, 15(1), 7-31.         [ Links ]

Brewer, W.F. (1987). Schemas versus mental models in human memory. Em: Borges, A. Tarciso. (1997). Um estudo de modelos mentais. Investigações em ensino de ciências, 2(3), 207-226.         [ Links ]

Eisenck, M.W. e Keane, M.T. (2007). Psicologia cognitiva: um manual introdutório. Porto Alegre: Artes Médicas.         [ Links ]

Fonseca, V. da. (2009). Cognição, neuropsicologia e aprendizagem. Petrópolis: Vozes.         [ Links ]

Ford, J.A. (1995). Two modes of mental representation and problem solution in syllogistic reasoning. Cognition, 54, 1-71. Em: Eisenck, M.W.; Keane, M.T. (1994). Psicologia cognitiva: um manual introdutório. Porto Alegre: Artes Médicas.         [ Links ]

Gardner, H. (2003). A nova ciência da mente. São Paulo: Editora da Universidade de São Paulo.         [ Links ]

Gentner, D. e Stevens, A.L. (Ed.). (1983). Mental models. Hillsdale: Lawrence Erlbaum Associates.         [ Links ]

Johnson-Laird, P. (1983). Mental models. Cambridge: Harvard University Press.         [ Links ]

Johnson-Laird, P. (1999). Deductive reasoning. Annual Review of Psychology, 50, 109-135. Em: Eisenck, M.W.; Keane, M.T. (1994). Psicologia cognitiva: um manual introdutório. Porto Alegre: Artes Médicas.         [ Links ]

Lagreca, M.C.B. e Moreira, M.A. (1999) Tipos de representações mentais utilizadas por estudantes de física geral na área de mecânica clássica e possíveis modelos mentais nessa área. Revista Brasileira de Ensino de Física, 21(1), 202-215.         [ Links ]

Lorenzato, S. (2008). Para aprender matemática. São Paulo: Autores associados.         [ Links ]

Moreira, M.A. (1997). Modelos Mentais. Em: Faculdade de Educação da UFMG (Org.), Anais, I Encontro Sobre Teoria e Pesquisa em Ensino de Ciência. Belo Horizonte: Faculdade de Educação, UFMG.         [ Links ]

Moreira, M.A. e Oliveira, A.P. (2003). Dificuldade dos alunos na aprendizagem da lei de Ampère, à luz da teoria dos modelos mentais de Johnson-Laird. Revista Brasileira de Ensino de Física, 25(3), 317-325.         [ Links ]

Norman, D.A. (1983). Some observations on mental models. Em: Gentner, D. e Stevens, A.L. (Ed.). (1983). Mental models (pp. 6-14). Hillsdale: Lawrence Erlbaum Associates.         [ Links ]

Sternberg, R.J. (2008). Psicologia cognitiva. Porto Alegre: Artmed.         [ Links ]

Vieira Junior, N. e Colvara, L. D. (2006). A importância do professor conforme estilos de aprendizagem e modelos mentais. Em: Associação Brasileira de Ensino de Engenharia (Org.), Anais, XXXIV Congresso Brasileiro de Ensino de Engenharia (pp. 1239-1250). Passo Fundo: ABENGE.         [ Links ]

 

Notas

N. Vieira Junior
Endereço para correspondência: Rua Padre Alberico, S/N, Bairro São Luiz, Formiga, MG 35.570-000.
Telefone para contato: +55-37-33214094.
E-mail para correspondência: niltom@gmail.com.

L. D. Colvara
Endereço para correspondência: Av. Brasil Centro, 56, Ilha Solteira, SP 15.385-000.
Telefone para contato: +55-18-37431150.
E-mail para correspondência: laurence@dee.feis.unesp.br.