Fundamentos matemáticos e cognitivos para o ensino de matemática para alunos deficientes mentais

 

 

Maria da Piedade Resende da Costa

Universidade Federal de São Carlos. Departamento de Psicologia Centro de Educação e Ciências Humanas

 

 

O ensino da matemática para o deficiente mental (moderado) é uma das preocupações da autora, surgida em conseqüência de estudos anteriormente realizados e divulgados em reuniões científicas como o XXII Interamerican Congress of Psychology (realizado em 1989 na cidade de Buenos Aires) e 16^th e 17^th Annual Convention - Association for Behavior Analysis (realizadas respectivamente em 1990 e 1991 nas cidades de Nashville e Atlanta).

O presente texto tem como objetivo destacar alguns pontos sobre o ensino da matemática para o deficiente mental (moderado). Ao tratar do ensino, a tendência da autora é a de direcionar sua preocupação para a vertente que se refere ao professor sem esquecer, contudo, a vertente de como ocorrem as aquisições pelo aluno. Nos estudos realizados, observando como a matemática é ensinada para o deficiente mental, a autora detectou um desconhecimento sobre o conteúdo de noções básicas por parte do professor e conseqüente prejuízo quanto às aquisições do aluno deficiente mental.

 

DIFERENTES ENFOQUES

A literatura, tanto no âmbito da Psicologia, quanto no da Educação, aponta uma vasta produção do conhecimento sobre o tema ensino/aprendizagem. Dentre as principais teorias que tratam deste tema encontram-se as de Bruner (1969 e 1973), Piaget (1959, 1973, 1976 e 1977), Rogers (1971 e 1978), Gagné (1971 e 1980), Skinner (1972, 1973 e 1974), Ausubel, Novak e Hanesian (1980).

De um modo geral, podem-se abstrair, dos citados autores, três grandes enfoques teóricos que tratam do processo ensino/aprendizagem: o humanístico, o cognitivista e o comportamentalista. Cada um destes enfoques teóricos tem influenciado diversas práticas educacionais através de aplicações de métodos, técnicas e procedimentos de ensino.

Particularmente, o ensino/aprendizagem da matemática tem sido objeto de estudo dos vários enfoques teóricos da psicologia. Assim, para a psicogenética, a aquisição mental do número não se dá por simples aprendizagem: depende das estruturas mentais que se sucedem ordenadamente na criança, através de etapas, desde uma idade bem tenra (Piaget e Szeminska, 1950; Piaget e Inhelder, 1962; Piaget e Inhelder, 1975 e Piaget, 1975). Segundo estes autores, para começar a operacionalizar o número conceitualmente, a criança deve estar perceptivelmente madura e ter determinadas estruturas operatórias mentais. Por meio de atos exploratórios, a criança verifica as relações numéricas: por exemplo, um conjunto constituído por quatro objetos é maior do que um constituído por dois objetos.

Entretanto, isto não ocorre com o aluno deficiente mental: uma forma de aprendizagem inadequada ocorre com este aluno no que se refere à contagem. Há uma falta de habilidade facilmente observada neste aluno. É comum ouvi-lo nomear a seriação: "Um, dois, três, quatro ..." atingindo numeração bem alta, sem conhecer o seu significado. Ele recebeu esta informação do ambiente e foi largamente reforçado por expressá-la de forma oral, e, às vezes, de forma gráfica; seu comportamento, no entanto, indica que, para ele, a contagem carece de qualquer significado. Caso este aluno continue a receber orientação inadequada, permanecerá expressando esta numeração sem compreender o significado da contagem.

Um outro tipo de contagem comumente encontrada no aluno deficiente mental é a descrita a seguir. Colocando-se sobre a mesa uma série de objetos (lápis, por exemplo) alinhados e solicitando-se a este aluno que faça a contagem, observa-se que ele a executa sem estabelecer correspondência entre a quantidade e a nomeação. Ele fala: "Um" colocando o dedo no primeiro objeto; fala "Dois" colocando o dedo no espaço existente entre o primeiro e o segundo objeto; fala: "Três" colocando o dedo no segundo objeto. Assim, continua a sua contagem nomeando inadequadamente a quantidade, por não haver correspondência com os objetos que conta.

Conforme estudos realizados (Piaget e Szeminska, 1950; Piaget, 1961; Piaget e Inhelder, 1962; Piaget e Inhelder, 1975 e Piaget, 1975), a aquisição do número pela criança normal é realizada lentamente e de forma progressiva. Esta criança, ao entrar para a escola, com aproximadamente 6 anos de idade cronológica, já realizou observações e experiências bem variadas. Isto lhe permite fazer aquisições sobre noções básicas e construções lógicas imprescindíveis para a aprendizagem da matemática.

Com o aluno deficiente mental, entretanto, isto não ocorre: ele não consegue adquirir as noções básicas para a aprendizagem da matemática devido à limitação de suas experiências e, conseqüentemente, tem dificuldades de efetuar as necessárias construções lógicas.

Esta incapacidade apresentada pelo aluno deficiente mental para o aprendizado da matemática já fazia parte da preocupação de Séguin quando publicou, em 1846, seu trabalho Traitment Moral, Hygiène et Éducation des Idiots et des Autres Enfants Arriérés.

Conforme Séguin (1846), o ensino da iniciação à matemática para o deficiente mental tinha como objetivo familiarizá-lo com as quantidades observáveis na vida prática. Assim, denominou a aritmética por ele ensinada ao aluno deficiente mental como a ciência dos números sensíveis. E, mais explicitamente, afirmou que: "Para meus alunos, um, dois, três, quatro devem ser coisas antes de serem quantidades; a idéia do número deve preceder sempre o símbolo assim como a criança fala as palavras antes de as ler" (Séguin, 1846, p.480). Esta frase expressa, exatamente, como Séguin procedeu para ensinar matemática para o aluno deficiente mental.

Montessori (1965), na proposição de seu método, também se preocupou com o ensino da numeração e iniciação à aritmética para o aluno deficiente mental, partindo do concreto. Assim, confeccionou um material específico para o ensino da matemática, como, por exemplo, dez barras que entre si mantêm uma relação de 1 à 10. A menor barra tem 10 cm, eqüivale ao primeiro segmento, é vermelha e representa a quantidade um. A segunda barra tem 20 cm, contém um primeiro segmento com 10 cm na cor vermelha e um segundo segmento com 10 cm na cor azul e corresponde à quantidade dois. A terceira barra de 30 cm de comprimento possui o primeiro segmento de 10 cm na cor vermelha, o segundo segmento de 10 cm na cor azul e o terceiro segmento de 10 cm na cor vermelha e eqüivale a quantidade três. E, assim, sucessivamente, até a barra com um metro de comprimento que representa a quantidade dez.

As barras confeccionadas por Montessori facilitam o cálculo porque, ao se colocar a barra indicativa da quantidade "um" ao lado da barra da quantidade "dois", obtém-se um comprimento igual à barra da quantidade "três"; ao mesmo tempo em que esta operação é realizada, ocorre o processo de síntese, ou seja, o aluno efetua uma adição.

Outro material confeccionado por Montessori (1965) para o ensino da matemática são os dez numerais (sinais gráficos dos números). Ela os confeccionou em lixa com a finalidade de proporcionar também a estimulação sensorial tátil. Os fusos e os cartões de 0 a 9 propostos por Montessori, em seu método, também são materiais que permitem ao aluno construir sua tabuada.

Como pode ser observado, Séguin (1846) e Montessori (1965), em seus estudos, preocuparam-se especificamente com o ensino da iniciação à matemática para o deficiente mental. Entretanto, um grande avanço ocorrido no ensino da matemática deu-se com os estudos realizados por Piaget e Szeminska, relatados no livro La Genèse du Nombre chez l'Enfant, publicado em 1950.

Segundo Piaget e Szeminska (1950), a base para a aquisição da noção geral do número encontra-se em noções anteriores como as de conservação, correspondência e equivalência. A aquisição de cada uma destas noções pela criança é realizada em três estágios sucessivos, ou seja, compreende desde a ausência (primeiro estágio), passando por uma etapa intermediária (segundo estágio) até a aquisição (terceiro estágio).

A noção de conservação, segundo Piaget e Szeminska (1950), "constitui uma condição necessária de toda atividade racional" (p.6). Conforme os estudos descritos por Piaget e Szeminska, os três estágios sucessivos para a aquisição da noção de conservação são:

1ª- estágio - Não conservação: "A criança não conserva as quantidades contínuas nem as coleções descontínuas, quando sua configuração perceptiva está alterada." (p.42)

2ª- estágio - Intermediário: "Caracteriza-se pelas soluções intermediárias situadas a meio caminho entre a quantidade bruta sem invariabilidade e a quantificação propriamente dita. A criança se inclina a aceitar a conservação e esta tendência entra em conflito com a aparência contrária." (p.42)

3ª estágio - Conservação: "A criança não tem que refletir para assegurar-se da conservação das quantidades totais: está segura a priori." (p.42).

Para as noções de correspondência e equivalência, Piaget e Szeminska (1950) também estabelecem três estágios sucessivos:

1ª estágio - Comparação global e ausência de correspondência;

2ª estágio - Correspondência termo a termo sem equivalência duradoura e,

3ª estágio - Correspondência termo a termo com equivalência duradoura.

Metton-Granier (1972), replicando os experimentos de Piaget, realizou um estudo sobre as noções de conservação, correspondência e equivalência com deficientes mentais. Os resultados obtidos sobre a noção de conservação permitiram constatar que o deficiente mental cuja idade mental é superior a 6 anos não tem, necessariamente, a noção de conservação. Ainda neste estudo, foram observados os problemas de linguagem (articulação incorreta das verbalizações) apresentados pelo deficiente mental. É possível que a constatação do estudo esteja atrelada aos problemas de linguagem apresentados pelos sujeitos.

Em relação às noções de correspondência e equivalência os resultados indicaram que a maior parte de deficientes mentais encontrava-se no segundo estágio. Assim, a correspondência desaparece quando se elimina a identidade das figuras formadas pelas duas coleções, indicando que o deficiente mental leva em consideração apenas o aspecto global.

A matemática ensinada para o aluno deficiente mental é a mesma matemática ensinada para qualquer aluno. Isto significa que o professor do aluno deficiente mental deve, também, conhecer os conceitos básicos da matemática, a fim de melhor aplicar os procedimentos de ensino.

 

NOÇÕES BÁSICAS DE MATEMÁTICA

Entre os conceitos básicos, faz-se necessário ao professor conhecer número/numeral, base e conjunto, temas estes que serão tratados a seguir.

Número/numeral

Na literatura existente sobre a origem dos números consta que o homem primitivo não conhecia o número, porém tinha a faculdade que o levava a julgar uma quantidade (Boyer, 1974). Poder-se-ia compará-lo a uma criança: diante de dois conjuntos de balas, escolherá o que tem mais balas (elementos). É uma habilidade visual que permite detectar onde há mais e onde há menos elementos.

É o número in diferenciado qualitativamente percebido. Serve a um pastor para compor quando chama seu rebanho. O pastor sabe se estão todas ou se faltam algumas ovelhas. Esta capacidade é denominada de apreensão de coleções e de grupos (Flournoy, 1968; Spitzer, 1970; Gomide, 1971 e Boyer, 1974).

Decroly (1929) descobriu, em suas investigações com criança de 1 ano, manifestações capazes de informar sobre as noções que se poderiam formar a respeito da quantidade e do número. Até os 14 meses a criança só pode jogar com três unidades, porém, ao chegar aos 14-16 meses, a criança aprende a manejar conjuntos mais extensos. Quando surge o nome, aparece no conjunto uma qualidade como, por exemplo, a do conjunto crianças; há uma sucessão ordenada dos nomes. A sucessão de nomes automatizada é a numeração. Assim, o passo da abstração numérica é o passo da coisa à qualidade numérica, que interessa mais que a própria coisa.

Imagina-se que, bem remotamente, o homem, para conferir o seu rebanho, fazia a correspondência entre um animal e uma pedrinha. Da prática desta abstração surgiu a noção de número. Daí, provavelmente, surgiram os sistemas de numeração: substituição das pedrinhas pelo uso dos dedos de uma mão e, posteriormente, da outra mão. Conseqüentemente, teve início o sistema de base cinco, ou seja, as unidades agrupadas de cinco em cinco.

Durante o decorrer da História existiram vários sistemas de numeração como o dos etruscos, romanos, babilônios, egípcios, gregos, maias e indo-arábicos.

Devido à relevante economia que oferece para expressar e computar as quantidades e à simplicidade, o sistema de numeração indo-arábico é o mais usado. Isto pode ser evidenciado no exemplo indicado na Figura 1.

 

 

Analisando o exemplo apresentado na Figura 1 pode-se observar que para representação do número (quantidade) quatro foram utilizados no numeral:

- indo-arábico:	um só símbolo
- romano:	dois símbolos
- maia:	um símbolo repetido quatro vezes
- babilônico	um símbolo repetido quatro vezes
- egípcio	um símbolo repetido quatro vezes

O sistema de numeração chama-se indo-arábico porque é originário da índia e chegou até a civilização européia através dos árabes. A grafia destes símbolos foi sistematizada pelo matemático árabe Al-Karismi, daí estes símbolos também receberem a denominação de algarismos. Portanto, convém ressaltar aqui que a expressão algarismos romanos utilizada em alguns livros de matemática é inadequada.

A demonstração contida no exemplo da Figura 1, em relação ao número (quantidade) e numerai (símbolo), pretende orientar o professor no que se refere ao ensino da iniciação à matemática para o aluno deficiente mental. E comum haver a introdução do ensino do símbolo (numeral) sem o referido aluno compreender o número.

O indo-arábico é um sistema exponencial-posicional: considera as potências de base e o valor do lugar dos algarismos.

Convém estabelecer a diferença entre sistema de numeração e sistema numérico. Enquanto aquele é o conjunto de símbolos usados para expressar os números, este é um conjunto de números, de operações definidas nesse conjunto e de regras que governam essas operações (Gomide, 1971, p.58).

Para representar todos os números o sistema de numeração indo-arábico usa dez símbolos: 1, 2, 3, 4, 5, 6, 7, 8, 9 e 0.

Base

Para o sistema de numeração indo-arábico, a base é 10 provavelmente determinada pela quantidade de dedos nas mãos: dez. Além da base 10, são usadas outras como: base 2 (binaria), base 5 (quinaria), base 12 (duodecimal).

A seguir encontra-se exemplificado como o número 3725 pode ser representado na:

base 10 = 3 x 10³ + 7 x 10² + 2 x 10 + 5 x 10⁰

base 12 = 2 x 12³ + 1 x 12² + 10 x 12 + 5 x 12⁰

base 5 = 1 x 5⁵ + 0 x 5⁴ + 4 x 5³ + 4 x 5² + 0 x 5 + 0 x 5⁰

base 2 = 1 x 2¹¹ + 1 x 2¹⁰ + 1 x 2⁹ + 0 x 2⁸ + 1 x 2⁷ + 0 x 2⁶ + 0 x 2⁵ + 0 x 2⁴ + 1 x 2³ + 1 x2² + 0 x x 2+ 1 x 2⁰

Qualquer que seja a base, obtêm-se cifras que indicam o número de vezes que se encontra uma mesma potência da base.

Para se obterem as diferentes bases de um número, existem dois métodos: dos subconjuntos e das divisões sucessivas. Método dos subconjuntos - Formação, em um conjunto dado e sucessivamente, de subconjuntos com n, n², n³, n⁴ ... elementos e escrita dos números na base correspondente.

Como exemplificação, a Figura 2 descreve um conjunto de 24 elementos nas bases 10, 5, 3 e 2.

 

 

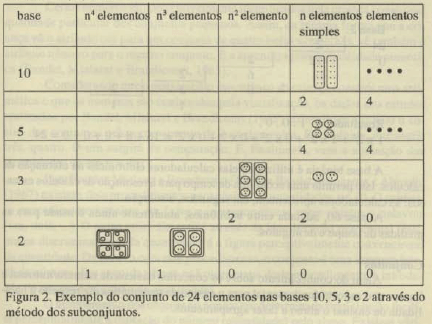
Método das divisões sucessivas - Este método permite efetuar o cálculo de base desejada a partir da base 10. Exemplificação com 24 elementos:

 

 

A base binaria é utilizada pelas calculadoras eletrônicas na efetuação de cálculos. Isto permite uma economia de tempo para a resolução de cálculos extensos: as calculadoras apresentam, em segundos, a solução.

A base 60, adotada entre babilônios, atualmente ainda é usada para as medidas de tempo e de ângulos.

Conjuntos

Além do conhecimento sobre os conceitos básicos de número/numerai e base, outro aspecto fundamental para o ensino da matemática diz respeito à habilidade de ensinar o aluno a fazer agrupamentos.

Para o aluno normal, a habilidade de fazer agrupamentos desenvolve-se natural e progressivamente, como foi visto anteriormente (Piaget e Szeminska, 1950). Porém, isto é problemático para o aluno deficiente mental devido à pobreza de vocabulário geralmente apresentada por este aluno. Compreender que uma rosa, um cravo e uma dália pertencem ao conjunto das flores é um processo lingüístico: vários objetos com características comuns são agrupados e recebem um novo termo mais econômico e generalizador (Feldman, 1982). Porém, compreender que o conjunto "flores" é maior do que o conjunto "rosas vermelhas" e que o conjunto "rosas vermelhas" pertence tanto ao conjunto "flores" quanto ao conjunto "objetos vermelhos", envolve conceitos mais complexos (Feldman, 1982). Os estímulos rosa, dália e cravo são perceptivelmente semelhantes. Entretanto, em estímulos perceptivelmente diferentes, dever-se-á aplicar devidamente procedimentos a fim de que o aluno deficiente mental atinja melhores níveis de generalização lingüística.

Para Dienes (1970 e 1977), existe um mundo intermediário entre o mundo dos objetos e o dos números: é o "mundo dos conjuntos". Daí, conjuntos devem ser ensinados a fim de fazer parte do repertório comportamental do aluno deficiente mental para que ele possa construir os números. Para isto, é necessário que o professor conheça a noção básica de conjunto.

Certos números são perceptivelmente identificados pela criança como uma qualidade particular dos conjuntos pequenos. Assim, da mesma forma que a criança vê o atributo cor para um conjunto de quatro bolas vermelhas, vê também o atributo número para o mesmo conjunto. É a aprendizagem da qualidade numérica (Bandet, Mialaret e Brandicourt, 1965).

Considerando que o pensamento espontâneo da criança constrói uma aritmética e que os números são conhecidos pela visualização, os dados dos estudos realizados por Bandet, Mialaret e Brandicourt (1965) aconselham a iniciar o ensino dos conjuntos pelo agrupamento de dois elementos. Em seguida, introduzir três, quatro. O um surgirá da comparação. E, finalmente, vem a aquisição das quantidades de cinco a dez.

Para Bandet, Mialaret e Brandicourt (1965) e Bandet, Sarazanas e Abbadie (1967) existem dois procedimentos para ensinar as quantidades até 10. O primeiro procedimento consiste em fazer a correspondência entre objetos e palavras (um, dois,...). O outro procedimento é através da identificação perceptual (estímulos discriminativos) da quantidade: é a figura perceptivelmente convencional da quantidade. De acordo com este procedimento, o conjunto é uma imagem falada do número. Em seguida, chega-se à outra etapa deste procedimento: a introdução do numerai (símbolo da quantidade).

O agrupamento dos objetos ou pontos em determinada organização facilita perceptualmente a captação do número (quantidade) pelo aluno. Existem vários modelos, mas aquele apresentado na Figura 3 oferece melhor visualização.

 

 

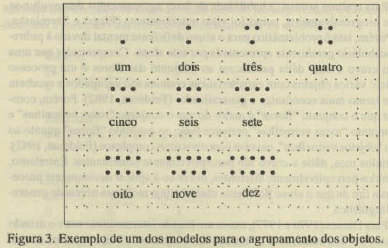
Observa-se que estes agrupamentos favorecem, perceptivelmente, o aluno a compreender que cada número sucede o antecedente pela adição de uma unidade. Além deste aspecto, já permite a formação dos pares (aquisição dos números pares e ímpares).

Assim, a noção de par e ímpar, também é perceptivelmente adquirida pelo aluno. E, ainda, perceptivelmente o aluno é capaz de aplicar a análise/ síntese (adição/subtração) como no exemplo indicado na Figura 4.

 

 

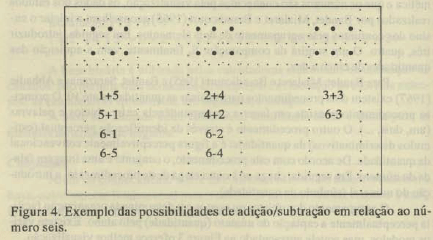
Observa-se que nas possíveis combinações associativas, por exemplo, do número quatro (3 + 1; 1 + 3; 2 + 2; 1 + 1 + 1 +1), o aluno esta aplicando o mesmo processo utilizado quando aprende, por exemplo, a palavra pato (pa + to; p + a + t + o). Isto evita que o aluno deficiente mental faça aquisições deficitárias e apresente erros semelhantes aos portadores de discalculia (Gerstmann, 1940; Cohn, 1961; Daurat-Hmeljak e Marlan, 1967; Cohn, 1968 e Guay e McDaniel, 1977). Isto ocorre porque, conforme explica Dienes (1977, p.15), "as relações entre conjuntos conduzem a considerações de natureza lógica, ao passo que as propriedades dos conjuntos levam a considerações de natureza matemática".

No ensino dos conjuntos, devem-se, então, utilizar procedimentos para que o aluno deficiente mental amplie seu repertório comportamental verbal, ou seja, a fim de que ele faça generalizações ao nível lingüístico. Para isto deve-se, inicialmente, fazer os agrupamentos por semelhança perceptiva absoluta e, em seguida, por função (Piaget e Inhelder, 1975 e Piaget, 1975).

Para Feldman (1982), antes de iniciar o procedimento para o estabelecimento de operações das classes entre si, o aluno deve: a) fazer agrupamentos sob um item conceitual comum; e, b) nomear cada classe adequadamente.

Piaget e Inhelder (1975) denominaram estruturas lógicas às estruturas classificatórias. Assim, a composição destas estruturas pode ser por agrupamento aditivo de classes, estrutura vicariante, multiplicação counívoca de classes e multiplicação biunívoca de classes.

O agrupamento aditivo de classes consiste na união de duas subclasses em uma classe comum. Portanto, gatos (subclasse) e patos (subclasse) pertencem a uma classe comum animais. Isto, conseqüentemente, permite duas outras operações: classes complementares e relação todo/parte.

Nas classes complementares, a operação lógica realizada é a seguinte; "o conjunto de objetos pode ser dividido em todos os elementos que pertencem a uma determinada classe e todos aqueles que não pertencem a ela" (Feldman, 1982, p.9). Como exemplo, pode ser citado um conjunto de frutas que pode ser dividido em bananas e não-bananas.

Quanto à relação todo/parte, pode-se estabelecer que, em duas subclasses, "o fato invariável, a classe maior, sempre tem mais elementos que a classe menor" (Feldman, 1982, p.9). Assim, laranjas e bananas formam um conjunto de frutas. Então, sempre há mais frutas do que laranjas e do que bananas.

A estrutura vicariante "permite a troca sucessiva de critério dentro de uma mesma classe" (Feldman, 1982, p.9). Uma classe, com efeito, é uma reunião de termos considerados como equivalentes independentemente de suas diferenças (Piaget e Szeminska, 1950): os vertebrados, por exemplo, podem ser aves e mamíferos grandes (ema, elefante) e pequenos (beija-flor, rato). No número (quantidade), a estrutura vicariante significa a propriedade associativa e dissociativa (Feldman, 1982, p.9) como: 7 = 6 + 1, 5 +2, 4 +3, 7 + 0

A multiplicação counívoca de classes "é a intersecção de conjuntos que permite situar um elemento em dois conjuntos simultaneamente" (Feldman, 1982, p.9). Assim, a bola pertence, ao mesmo tempo, ao conjunto dos brinquedos e ao dos corpos esféricos; a rosa vermelha pertence, ao mesmo tempo, ao conjunto das flores e ao conjunto dos objetos vermelhos.

Quando uma classe total pode estar dividida conforme critérios diferentes verifica-se a multiplicação biunívoca de classes. Na prática, são os exercícios do quadro de dupla entrada (ver Figura 5):

 

 

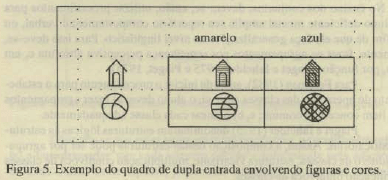
Este tipo de exercício favorece o processo de análise/síntese implicando facilitação para análise/síntese no âmbito da leitura conforme o exemplo indicado na Figura 6.

 

 

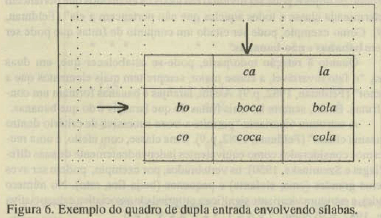
O professor, ao estudar as noções básicas, passará a aplicar procedimentos de ensino investindo na aquisição por parte do aluno deficiente mental, inclusive na sua compreensão lingüística.

 

CONCLUSÕES

O presente texto permite concluir que para que a matemática seja ensinada ao aluno deficiente mental, cabe ao professor conhecer as noções básicas de matemática. Isto porque, conhecendo estas noções, poderá compreender, também, como as aquisições são realizadas por parte do aluno deficiente mental e aplicar procedimentos de ensino que propiciem a este aluno a realizar construções lógicas.

Permite concluir, ainda, que ao ensinar matemática para o aluno deficiente mental, o professor estará favorecendo o processo de análise/síntese importante para a aquisição da leitura.

E, finalmente, o texto permite concluir que o ensino da matemática não é um fim em si mesmo: tem um objetivo mais ambicioso, ou seja, propiciar o desenvolvimento da competência lingüística do aluno deficiente mental e, conseqüentemente, o desenvolvimento de seu potencial cognitivo.

 

Referências Bibliográficas

Ausubel, D.P.; Novak, J.D. e Hanesiah, H. (1980) Psicologia Educacional. Rio de Janeiro: Interamericana.         [ Links ]

Bandetl, J.; Mialaret, G. e Brandicourt, R. (1965) Les Débuts du Calcul. Paris: Librairie Armand Colin.         [ Links ]

Bandet, J.; Sarazanas, R. e Abbadie, M. (1967) Vers l'Aprentissage des Mathématiques. Paris: Librairie Armand Colin.         [ Links ]

Boyer, C.B. (1974) História da Matemática. São Paulo: Edgard Blucher.         [ Links ]

Bruner, J.S. (1969) Uma nova Teoria da Aprendizagem. Rio de Janeiro: Bloch.         [ Links ]

Bruner, J.S. (1973) O Processo de Educação. São Paulo: Nacional.         [ Links ]

Cohn, R. (1961) Dyscalculia. Archives of Neurology, 4, 301-307.         [ Links ]

Cohn, R. (1968) Developmental dyscalculia. Pediatric Clinics of North America, 15(3), 651-668.         [ Links ] Daurat-Hmeljak, C. e Marlan, R. (1967) Rééducation du calcul. La Psychiatrie de l'Enfant, S.l., 10, 399-555.         [ Links ]

Decroly, O. (1929) Problemas de Psicologia y de Pedagogia. Madri: Francisco Beltrán Libreria Espanola y Extranjera.         [ Links ]

Dienes, Z.P (1970) Aprendizado Moderno da Matemática. Rio de Janeiro: Zahar.         [ Links ]

Dienes, Z.P. (1977) A Matemática Moderna no Ensino Primário. Lisboa: Livros Horizonte Ltda.         [ Links ]

Feldman, J. (1982) Aritmética para Crianças com Problemas de Linguagem. Rio de Janeiro: Enelivros.         [ Links ]

Flournoy, F. (1968) Las Matemáticas en la Escuela Primária. Buenos Aires: Troquel S.A.         [ Links ]

Gagné, R.M. (1971) Como se Realiza a Aprendizagem. Rio de Janeiro: Livro Técnico.         [ Links ]

Gagné, R.M. (1980) Princípios Essenciais da Aprendizagem para o Ensino. Porto Alegre: Globo.         [ Links ]

Gerstmann, J. (1940) Syndrome of finger agnosia, disorientation for right and left, agraphia and acalculia. Articles of Neurology and Psychiatry, monografhy.         [ Links ]

Gomide, M.V. (1971) Explorando a Matemática na Escola Primária. Rio de Janeiro: José Olympio.         [ Links ]

Guay, R.B. e McDaniel, E.D. (1977) The relationship between mathematics achievement and spatial abilities among elementary school children. Journal for Research in Mathematics Education, 211-215.         [ Links ]

Metton-Granier, M. (1972) La aquisición de la noción de número en el nino deficiente mental. Em Transtornos del Aprendizaje del Calculo. Barcelona.         [ Links ]

Montessori, M. (1965) Pedagogia Científica: a Descoberta da Criança. São Paulo: Flamboyant.         [ Links ]

Piaget, J. (1959) A Linguagem e o Pensamento da Criança. Rio de Janeiro: Fundo de Cultura S.A.         [ Links ]

Piaget, J. (1961) L'Enseignement des Mathématiques. Paris: Editions Delachaux & Niestlé         [ Links ].

Piaget, J. (1973) A Epistemologia Genética. Rio de Janeiro: Vozes.         [ Links ]

Piaget, J. (1975) A Construção Real na Criança. Rio de Janeiro: Zahar.         [ Links ]

Piaget, J. (1976) A Equilibração das Estruturas Cognitivas. Rio de Janeiro: Zahar.         [ Links ]

Piaget, J. (1977) Psicologia da Inteligência. Rio de Janeiro: Zahar.         [ Links ]

Piaget, J. e Szeminska, A. (1950) La Genèse du Nombre chez l'Enfant. Paris: Delachaux et Niestlé         [ Links ].

Piaget, J. e Inhelder, B. (1962) La Représentation de l'Éspace chez l'Enfant. Paris: Press Universitaires de France.         [ Links ]

Piaget, J. e Inhelder, B. (1975) O Desenvolvimento das Quantidades Físicas na Criança. Rio de Janeiro: Zahar.         [ Links ]

Rogers, CR. (1971) Liberdade para Aprender. Belo Horizonte: Interlivros.         [ Links ]

Rogers, CR. (1918) Tomar-se Pessoa. São Paulo: Martins Fontes.         [ Links ]

Séguin, E. (1846) Traitment Moral, Higiéne et Education des Idiots des Autres Enfant Arriéres. Paris: Libraire de L'Academie Royale de Medicine.         [ Links ]

Skineer, B.F. (1972) Tecnologia do Ensino. São Paulo: Herder/ EPU/EDUSP, São Paulo.         [ Links ]

Skinner, B.F. (1973) O Mito da Liberdade. Rio de Janeiro: Bloch.         [ Links ]

Skinner, B.F. (1974) Ciência e Comportamento Humano. São Paulo: EDART-EDUSP.         [ Links ]

Spitzer, H.F. (1970) Ensenanza de la Aritmética. Buenos Aires: Libreria del Colégio.         [ Links ]