Serviços Personalizados
artigo
Indicadores
Compartilhar
Avaliação Psicológica
versão impressa ISSN 1677-0471versão On-line ISSN 2175-3431
Aval. psicol. vol.21 no.2 Campinas abr./jun. 2022
http://dx.doi.org/10.15689/ap.2022.2102.ed
EDITORIAL
O uso da inferência Bayesiana em análises psicométricas
Víthor Rosa Franco
Universidade São Francisco, Campinas - SP, Brasil. https://orcid.org/0000-0002-8929-3238
Por que utilizar a abordagem Bayesiana ao invés da abordagem estatística convencional em análises psicométricas? Essa é uma pergunta que permite diversas respostas diferentes, inclusive respostas que sugerem que métodos inferenciais Bayesianos não deveriam ser usados. De fato, a discussão sobre se a abordagem Bayesiana oferece algum tipo de vantagem em relação à abordagem estatística convencional (muitas vezes nomeada de frequentista) é complexa demais para ser tratada em um único texto (sugiro a leitura de Samaniego, 2010). Assim, longe de tentar dar uma resposta definitiva à pergunta inicial, irei definir o que são modelos estatísticos, discutir brevemente métodos de estimação frequentista e Bayesiana e, por fim, usar um exemplo para ilustrar possíveis vantagens dos métodos Bayesianos em análises psicométricas.
Tanto a abordagem Bayesiana quanto a abordagem frequentista proveem fundamentos para se testar modelos estatísticos. Modelos estatísticos são modelos matemáticos que incorporam pressupostos relacionados à incerteza sobre o processo que gerou os dados observados (Kruschke, 2014). Os modelos estatísticos são compostos de três componentes principais: (i) as variáveis as quais se pretende descrever, predizer ou explicar; (ii) os parâmetros que determinam os aspectos das relações entre as variáveis; e (iii) as relações funcionais entre variáveis e entre variáveis e parâmetros. Um exemplo bastante convencional é o modelo de regressão linear, onde se assume que o efeito de um conjunto de variáveis, definido por X, interagem aditivamente para causar variações em uma variável critério, y, conforme a seguinte equação:

onde β representa os parâmetros que definem os efeitos de cada variável no conjunto X e ε representa o erro, ou incerteza, sobre a relação entre X e y.
O objetivo da modelagem estatística é descobrir quais os valores de β e ε que melhor representam os dados e que podem ser generalizados para a população. De fato, resultados teóricos em estatística demonstram que a melhor estimativa para os parâmetros de um modelo é aquela que melhor representa os dados (Rossi, 2018). Os métodos de estimação que geram esse tipo de estimativa são chamados de métodos de "estimação da máxima verossimilhança". Esse nome expressa o fato de que esses métodos geram resultados que maximizam a similaridade entre os valores que podem ser gerados por um modelo e os valores observados de fato nos dados. Para se utilizar esses métodos em um modelo de regressão, por exemplo, é necessário modificar o modelo expresso na Equação 1 conforme pressupostos sobre a distribuição da variável critério y quando condicionada ao conjunto de variáveis X. Uma prática convencional resulta no seguinte modelo:

Essa representação do modelo diz que a variável y segue uma distribuição normal com a média determinada por Xβ e com a variância determinada por σ2. O parâmetro σ2 também é conhecido como a variância condicional de y e ela representa qual o tamanho médio do erro no modelo ou a variância que não pode ser explicada pelas variáveis em X. De forma mais geral, um modelo de regressão pode ser representado de forma não-paramétrica como:


onde Y representa o conjunto de variáveis critério e ? representarepresenta o conjunto de parâmetros do modelo que se pretende testar.
A partir dessa perspectiva, define-se modelos psicométricos a partir da Equação 4 como:

onde L representa um conjunto de variáveis latentes (ou seja, não-observadas). Assim, por exemplo, um modelo de análise fatorial pode ser definido como

onde yj representa o item j do instrumento psicométrico, j representa as cargas fatoriais que relacionam o conjunto de variáveis latentes L ao item yi e σ2j erepresenta a variância não explicada pelas variáveis latentes para o item yj. Em outro exemplo, o modelo de Rasch pode ser definido como:

onde θ representa a variável latente (ou escore verdadeiro, ou aptidão) e δj representa a dificuldade do item yi . A palavra Bernoulli é usada para representar que cada item no instrumento psicométrico segue a distribuição de Bernoulli, a qual deve ser utilizada quando os dados são binários (Agresti, 2018).
Após se definir o modelo estatístico que queremos ajustar, é necessário aplicar um algoritmo de otimização (Cortez, 2014) para se gerar os resultados. Na abordagem frequentista, são usados algoritmos como o algoritmo de maximização de expectativa, gradiente ascendente, o algoritmo de Broyden-Fletcher-Goldfarb-Shanno, entre outros. Independente de qual algoritmo é utilizado, o resultado é uma estimativa pontual para cada parâmetro do modelo. No entanto, pela estatística ser a ciência da incerteza, também é razoável supor que existe alguma incerteza em relação aos parâmetros que estão sendo estimados a partir dos dados e do modelo definido. Formalmente, essa incerteza pode ser representada como

A Equação 8 diz que a distribuição dos parâmetros-ou em outras palavras, a incerteza em relação ao valor dos parâmetros-depende dos valores das variáveis observadas. A abordagem frequentista não provem de métodos para estimar diretamente a distribuição de incerteza em relação aos parâmetros. Assim, para que se possa estimar a incerteza aos parâmetros nessa abordagem, são desenvolvidas teorias sobre o efeito da amostragem sobre os resultados encontrados nos estudos (para mais detalhes, ver Hoekstra et al., 2016).
Por outro lado, a abordagem Bayesiana parte do teorema de Bayes, o qual define a seguinte relação de proporcionalidade:

A Equação 9 pode ser separada em seus componentes principais. P( ? |Y,X) é a distribuição de incerteza dos parâmetros condicionada nas variáveis observadas, conhecida na abordagem Bayesiana como a distribuição posterior.  é a distribuição das variáveis em Y condicionada nas variáveis em X e nos parâmetros em ? , conhecida na abordagem Bayesiana como a verossimilhança. Por fim,
é a distribuição das variáveis em Y condicionada nas variáveis em X e nos parâmetros em ? , conhecida na abordagem Bayesiana como a verossimilhança. Por fim, 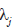 é a distribuição de incerteza dos parâmetros antes de se considerar os dados observados, conhecida na abordagem Bayesiana como a distribuição a priori. Assim, a Equação 9 diz que a distribuição de incerteza em relação aos parâmetros após se realizar uma análise é proporcional ao produto das probabilidades dos dados e da distribuição de incerteza em relação aos parâmetros antes de se realizar uma análise. Em termos mais diretos, a Equação 9 demonstra que é possível estimar a distribuição de incerteza dos parâmetros a partir dos dados de sua pesquisa.
é a distribuição de incerteza dos parâmetros antes de se considerar os dados observados, conhecida na abordagem Bayesiana como a distribuição a priori. Assim, a Equação 9 diz que a distribuição de incerteza em relação aos parâmetros após se realizar uma análise é proporcional ao produto das probabilidades dos dados e da distribuição de incerteza em relação aos parâmetros antes de se realizar uma análise. Em termos mais diretos, a Equação 9 demonstra que é possível estimar a distribuição de incerteza dos parâmetros a partir dos dados de sua pesquisa.
Assim, para se estimar uma versão Bayesiana do modelo de Rasch, por exemplo, é necessário complementar as informações da Equação 7 com distribuições a priori para os parâmetros do modelo. Uma alternativa possível (Fox, 2010) é:

Nessa versão do modelo, estamos estabelecendo que, antes de vermos os dados, tanto as aptidões dos indivíduos quanto as dificuldades dos itens têm como valor mais provável 0, sendo que a probabilidade de outros valores é determinada por uma distribuição normal com média igual a 0 e variância igual a 1.
A estimação dos parâmetros do modelo representado na Equação 10 podem ser estimados de duas formas principais. A primeira delas é pela aplicação dos mesmos algoritmos descritos anteriormente. Nesse caso, serão geradas estimativas pontuais, conhecidas como estimativas máximas posterior (maximum a posteriori estimation, MAP). Esse tipo de procedimento está implementado em alguns pacotes estatísticos para se estimar os valores da aptidão dos indivíduos após ter se estimado os parâmetros dos itens com métodos de estimação marginal. A similaridade entre as estimativas MAP e as estimativas de máxima verossimilhança aumentam conforme as distribuições a posteriori estabelecem menos certeza sobre os valores a priori dos parâmetros. Por exemplo, caso a variância dos parâmetros de dificuldade e aptidão fossem iguais a 100, ao invés de 1, as estimativas MAP desse modelo seriam mais parecidas com as estimativas de máxima verossimilhança.
A segunda forma de se estimar os parâmetros em uma abordagem Bayesiana envolve o uso de algoritmos mais complexos de otimização, os quais aproximam toda a distribuição posterior dos parâmetros, não apenas a estimativa MAP. Esses algoritmos podem funcionar de forma randômica ou determinística (p.ex., van Niekerk & Rue, 2021). Entre os algoritmos determinísticos os mais conhecidos são a aproximação de Laplace e os métodos variacionais. Entre os algoritmos randômicos (também nomeados como baseados em amostragem), os mais conhecidos são aqueles da família de cadeias de Markov de Monte Carlo (Markov chain Monte Carlo, MCMC). Os algoritmos MCMC são os algoritmos mais utilizados para a estimação Bayesiana. Isso provavelmente se deve por dois motivos principais. Primeiro porque os algoritmos MCMC, de acordo com a lei dos grandes números, sempre irão convergir à distribuição que representa a incerteza posterior aos parâmetros. A quantidade de iterações necessárias para se alcançar a convergência pode ser gigante, mas ela é garantida. O segundo motivo é que existem diversos programas, como o JAGS e o Stan, que facilitam a implementação de modelos Bayesianos para serem estimados com algoritmos de MCMC (para aprender mais sobre como usar esses programas, consultar Kruschke, 2014).
A partir desses fundamentos já podemos buscar uma forma de definir algumas das vantagens do uso de métodos Bayesianos em análises psicométricas. Iremos ilustrar tais vantagens pela implementação de um modelo de Rasch a dados aleatórios com 500 casos e 50 itens no software R. Para a estimação do modelo Bayesiano, usaremos o software JAGS e para estimação do modelo convencional usaremos o pacote mirt. O código para replicar as análises está disponível em: https://github.com/vthorrf/editorial212Bayes. Após ajustar os modelos, índices de ajuste e estatísticas descritivas em relação aos parâmetros dos indivíduos foram calculadas para os modelos Bayesiano e frequentista. Os principais resultados são apresentados na Figura 1.
Para o modelo Bayesiano calculamos quatro índices: (i) a precisão a posterior das distribuições dos parâmetros (Prec); (ii) a divergência de Kullback-Leibler entre a distribuição a priori e a distribuição posterior (KLD); (iii) a acurácia das estimativas médias feitas pelo modelo (Acc); e (iv) a informação de Fisher (FisherB). Para o modelo frequentista, calculamos quatro estatísticas de ajuste para as pessoas: (i) outfit, impacto de observações outlier (ou seja, respostas corretas a itens muito difíceis ou respostas erradas a itens muito fáceis); (ii) infit, impacto de observações triviais (ou seja, próximas à aptidão do indivíduo); (iii) Zh, uma medida padronizada da diferença média entre o valor observado e o valor esperado para uma resposta de um indivíduo específico ao conjunto de itens; e (iv) a informação de Fisher (FisherF).
Para se calcular os índices descritos, foi necessário usar estimativas dos escores verdadeiros. Para o modelo frequentista, os escores foram estimados com o método MAP. Para o modelo Bayesiano, os escores foram estimados com o método de expectância posterior (expected a posteriori, EAP). Como os dados foram simulados, também apresentamos o escore verdadeiro (true) na Figura 1. Para estimar as relações entre os índices de ajuste e entre esses e as estimativas do escore verdadeiro e o escore verdadeiro, foram usadas de correlação de distância (Székely et al., 2007). A correlação de distância é uma medida de dependência entre duas variáveis que é capaz de identificar associações lineares e não-lineares entre variáveis. Quando o valor é igual a 0, as variáveis são independentes. Quando o valor é igual 1, as variáveis são completamente dependentes.
Entre os resultados apresentados na Figura 1, vale ressaltar que os índices relacionados ao modelo Bayesiano de precisão, KLD e informação de Fisher apresentaram maior dependência com os escores verdadeiros do que a informação de Fisher do modelo frequentista. Isso significa que, apesar das dependências entre as estimativas dos escores (EAP e ML) terem igual dependência com os escores verdadeiros (true), os escores estimados pelo método Bayesiano são mais informativos sobre os padrões de resposta do que os escores estimados pelo método frequentista (mesmo que por uma pequena diferença). Por fim, cabe ressaltar que essa é uma exposição muito breve das capacidades dos modelos Bayesianos e que uma literatura extensa está disponível para aqueles que gostariam de se aprofundar na temática (por exemplo, Fox, 2010; Kruschke, 2014; Samaniego, 2010).
Referências
Agresti, A. (2018). An introduction to categorical data analysis. John Wiley & Sons. [ Links ]
Cortez, P. (2014). Modern optimization with R. Springer. [ Links ]
Fox, J. P. (2010). Bayesian item response modeling: Theory and applications. New York: Springer. [ Links ]
Hoekstra, R., Morey, R. D., Rouder, J. N., & Wagenmakers, E. J. (2014). Robust misinterpretation of confidence intervals. Psychonomic Bulletin & Review, 21(5), 1157-1164. https://doi.org/10.3758/s13423-013-0572-3 [ Links ]
Kruschke, J. (2014). Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Academic Press. [ Links ]
Rossi, R. J. (2018). Mathematical statistics: an introduction to likelihood based inference. John Wiley & Sons [ Links ]
Samaniego, F. J. (2010). A comparison of the Bayesian and frequentist approaches to estimation. Springer. [ Links ]
Székely, G. J., Rizzo, M. L., & Bakirov, N. K. (2007). Measuring and testing dependence by correlation of distances. The Annals of Statistics, 35(6), 2769-2794. https://doi.org/10.1214/009053607000000505 [ Links ]
Van Niekerk, J., & Rue, H. (2021). Correcting the Laplace Method with Variational Bayes. arXiv preprint arXiv:2111.12945. [ Links ]














